Edit me

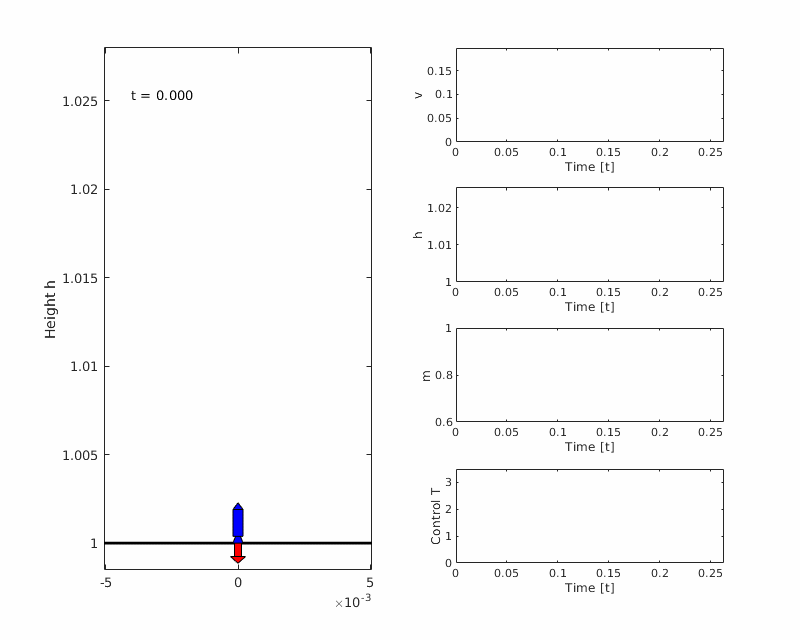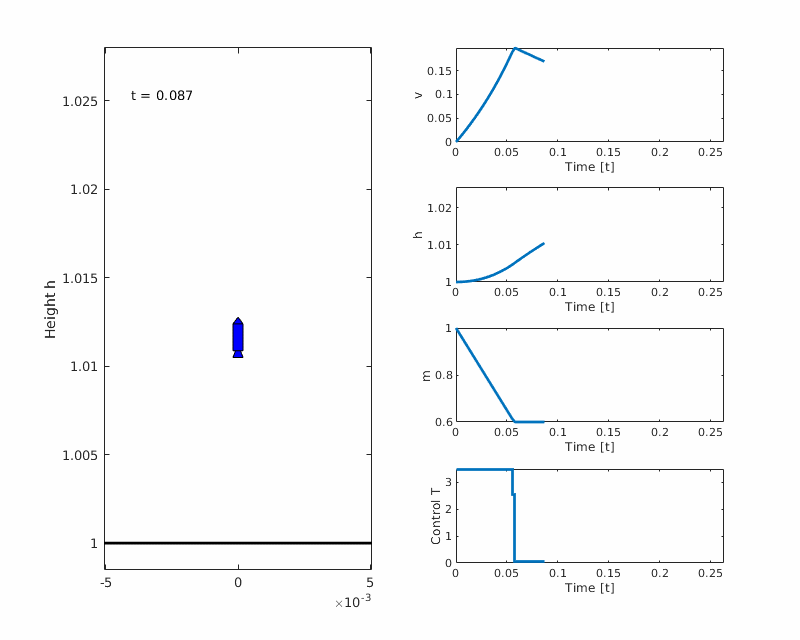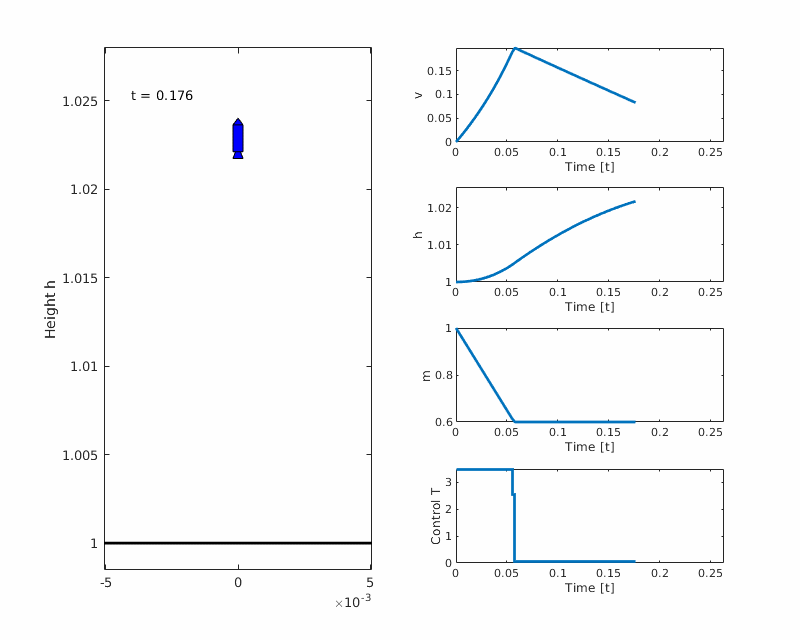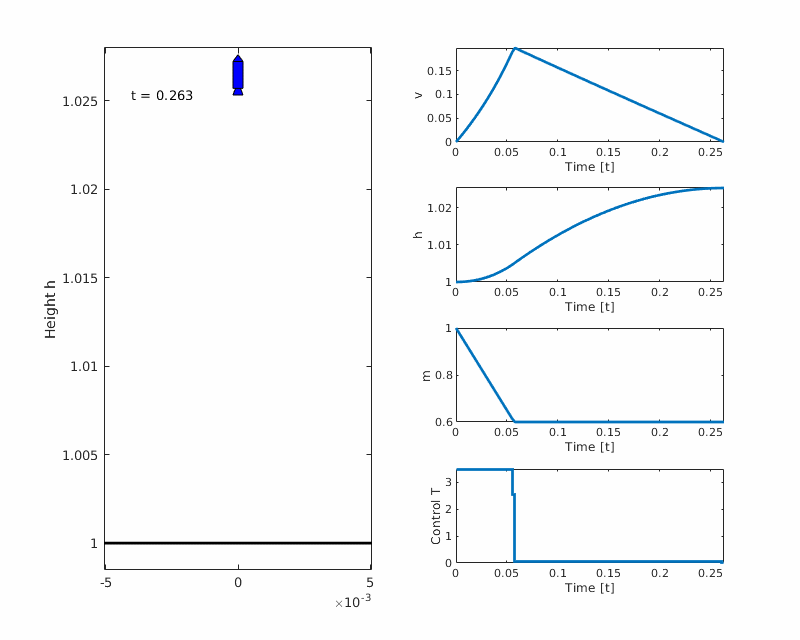
The Goddard rocket problem is an optimal control problem where the goal is to maximize the altitude of a vertically launched rocket, using thrust as control. This example is taken from the PROPT manual example 43.

Goddard Rocket Maximum Ascent Animation

Problem formulation

The problem formulation is the following:

$$\max \: h(t_{f})$$ $$\dot{v} = \frac{T-D(h,v)}{m}-g(h)$$ $$\dot{h} = v$$ $$\dot{m} = - \frac{T}{c}$$ $$D(h,v) = D_0 v^2 exp\Big( -\beta \Big( \frac{h-h(0)}{h(0)} \Big) \Big)$$ $$g(h) = g_0\Big(\frac{h(0)}{h} \Big)^2$$ $$m(0) = 1$$ $$m(t_f) = 0.6$$ $$v(0) = 0$$ $$h(0) = 1$$ $$g_0 = 1$$ $$0 \leq T \leq 3.5$$ $$D_0 = 0.5*620$$ $$c = 0.5$$ $$\beta = 500$$

The states are the rocket velocity $v$, the altitude from the center of the earth $h$ and mass of the rocket $m$. The rocket burns fuel and expels it out the nozzle creating thrust, in the model thrust $T$ is the control and the ratio between thrust and change in mass is $\dot{m} = -\frac{T}{c}$.

Yop implementation

%% Goddard Rocket, Maximum Ascent
% Author: Dennis Edblom
sys = YopSystem(...
    'states', 3, ...
    'controls', 1, ...
    'model', @goddardModel ...
    );
time = sys.t;

% Rocket signals (symbolic)
rocket = sys.y.rocket;

% Formulate optimal control problem
ocp = YopOcp();
ocp.max({ t_f( rocket.height ) });
ocp.st(...
     'systems', sys, ...
     ... % Initial conditions
    {   0  '==' t_0( time )              }, ...
    {   1  '==' t_0( rocket.height   )   }, ...
    {   0  '==' t_0( rocket.speed    )   }, ...
    {   1  '==' t_0( rocket.fuelMass )   }, ...
    ... % Constraints
    {   0  '<=' t_f( time )     '<=' inf  }, ...
    {   1  '<=' rocket.height   '<=' inf  }, ...
    { -inf '<=' rocket.speed    '<=' inf  }, ...
    {  0.6 '<=' rocket.fuelMass '<='  1   }, ...
    {   0  '<=' rocket.thrust   '<=' 3.5  } ...
    );

% Solving the OCP
sol = ocp.solve('controlIntervals', 100);

% Plot the results
figure(1)
subplot(311); hold on
sol.plot(time, rocket.speed)
xlabel('Time')
ylabel('Speed')

subplot(312); hold on
sol.plot(time, rocket.height)
xlabel('Time')
ylabel('Height')

subplot(313); hold on
sol.plot(time, rocket.fuelMass)
xlabel('Time')
ylabel('Mass')

figure(2); hold on
sol.stairs(time, rocket.thrust)
xlabel('Time')
ylabel('Thrust (Control)')

%% Model implementation
function [dx, y] = goddardModel(t, x, u)
% States and controls
v = x(1);
h = x(2);
m = x(3);
T = u;

% Parameters
c = 0.5;
g0 = 1;
h0 = 1;
D0 = 0.5*620;
b = 500;

% Drag
g = g0*(h0/h)^2;
D = D0*exp(-b*h);
F_D = D*v^2;

% Dynamics
dv = (T-sign(v)*F_D)/m-g;
dh = v;
dm = -T/c;
dx = [dv;dh;dm];

% Signals y
y.rocket.speed = v;
y.rocket.height = h;
y.rocket.fuelMass = m;
y.rocket.thrust = T;
y.drag.coefficient = D;
y.drag.force = F_D;
y.gravity = g;
end

Plots

Goddard Rocket Maximum Ascent States

Goddard Rocket Maximum Ascent Control

Yes     No

Give additional feedback below.